1 4 Of 20 Equals

Binary Estimator

Employ the following calculators to perform the addition, subtraction, multiplication, or division of 2 binary values, every bit well equally convert binary values to decimal values, and vice versa.

Binary Calculation—Add, Subtract, Multiply, or Divide

= ?

Catechumen Binary Value to Decimal Value

Binary Value: = ?

Catechumen Decimal Value to Binary Value

Decimal Value: = ?

The binary organization is a numerical system that functions virtually identically to the decimal number system that people are likely more familiar with. While the decimal number system uses the number x as its base, the binary system uses 2. Furthermore, although the decimal system uses the digits 0 through 9, the binary organization uses just 0 and 1, and each digit is referred to as a bit. Apart from these differences, operations such every bit addition, subtraction, multiplication, and division are all computed post-obit the same rules as the decimal system.

Almost all modern technology and computers utilize the binary system due to its ease of implementation in digital circuitry using logic gates. It is much simpler to design hardware that just needs to detect ii states, on and off (or truthful/false, nowadays/absent-minded, etc.). Using a decimal system would require hardware that can detect x states for the digits 0 through 9, and is more than complicated.

Below are some typical conversions betwixt binary and decimal values:

Binary/Decimal Conversion

Decimal	Binary
0	0
1	1
two	10
three	11
4	100
7	111
8	1000
10	1010
16	10000
xx	10100

While working with binary may initially seem disruptive, understanding that each binary place value represents 2^{due north}, merely as each decimal identify represents 10^{due north}, should help clarify. Have the number eight for example. In the decimal number organization, 8 is positioned in the beginning decimal place left of the decimal point, signifying the 10⁰ identify. Essentially this means:

eight × 10⁰ = viii × 1 = 8

Using the number 18 for comparison:

(i × 10¹) + (8 × ten⁰) = x + 8 = eighteen

In binary, 8 is represented as m. Reading from right to left, the starting time 0 represents 2⁰, the 2nd 2ⁱ, the third 2ⁱⁱ, and the fourth ii³; just similar the decimal organization, except with a base of ii rather than ten. Since two³ = 8, a ane is entered in its position yielding one thousand. Using 18, or 10010 as an example:

18 = sixteen + 2 = 2^four + two¹
10010 = (1 × two^four) + (0 × 2³) + (0 × 2^two) + (1 × iiⁱ) + (0 × ii⁰) = 18

The step by footstep procedure to catechumen from the decimal to the binary organisation is:

1. Discover the largest power of 2 that lies within the given number
2. Subtract that value from the given number
3. Find the largest power of ii within the residue found in step two
4. Repeat until there is no residual
5. Enter a 1 for each binary place value that was establish, and a 0 for the residue

Using the target of 18 again as an instance, below is another way to visualize this:

2n	24	2three	ii2	21	ii0
Instances within 18	ane	0	0	one	0
Target: 18	18 - 16 = 2	→		2 - 2 = 0

Converting from the binary to the decimal system is simpler. Make up one's mind all of the identify values where 1 occurs, and find the sum of the values.

EX: 10111 = (1 × 2⁴) + (0 × 2³) + (1 × two²) + (1 × 2¹) + (i × 2⁰) = 23

2four	23	2two	ii1	20
1	0	1	i	one
sixteen	0	4	2	1

Hence: sixteen + four + 2 + 1 = 23.

Binary Addition

Binary improver follows the same rules as add-on in the decimal system except that rather than carrying a i over when the values added equal ten, conduct over occurs when the outcome of addition equals 2. Refer to the example below for clarification.

Annotation that in the binary organisation:

0 + 0 = 0
0 + ane = 1
1 + 0 = 1
i + 1 = 0, carry over the one, i.e. 10

EX:

		10	1ane	ane1	10	ane
+		ane	0	one	1	1
=	1	0	0	1	0	0

The only real deviation between binary and decimal improver is that the value 2 in the binary system is the equivalent of 10 in the decimal system. Note that the superscripted one's represent digits that are carried over. A common error to watch out for when conducting binary addition is in the example where 1 + 1 = 0 also has a one carried over from the previous column to its right. The value at the bottom should so be 1 from the carried over 1 rather than 0. This tin be observed in the tertiary column from the right in the above example.

Binary Subtraction

Similar to binary addition, there is little difference between binary and decimal subtraction except those that arise from using merely the digits 0 and 1. Borrowing occurs in any instance where the number that is subtracted is larger than the number it is existence subtracted from. In binary subtraction, the only case where borrowing is necessary is when 1 is subtracted from 0. When this occurs, the 0 in the borrowing column essentially becomes "two" (irresolute the 0-1 into ii-ane = i) while reducing the 1 in the column beingness borrowed from by 1. If the following column is also 0, borrowing will take to occur from each subsequent column until a column with a value of 1 tin be reduced to 0. Refer to the example below for clarification.

Note that in the binary system:

0 - 0 = 0
0 - 1 = i, borrow ane, resulting in -i carried over
1 - 0 = i
1 - one = 0

EX1:

		-ane1	20	one	1	1
–		0	1	1	0	one
=		0	one	0	1	0

EX2:

		-i1	2-ane0	0
–		0	1	ane
=		0	0	ane

Note that the superscripts displayed are the changes that occur to each bit when borrowing. The borrowing column essentially obtains ii from borrowing, and the column that is borrowed from is reduced by 1.

Binary Multiplication

Binary multiplication is arguably simpler than its decimal counterpart. Since the simply values used are 0 and one, the results that must be added are either the same as the beginning term, or 0. Note that in each subsequent row, placeholder 0's demand to exist added, and the value shifted to the left, just like in decimal multiplication. The complication in binary multiplication arises from boring binary addition dependent on how many bits are in each term. Refer to the example below for clarification.

Note that in the binary system:

0 × 0 = 0
0 × 1 = 0
ane × 0 = 0
ane × 1 = 1

EX:

			1	0	1	1	1
×						1	ane
			1	0	1	1	1
+		ane	0	i	1	1	0
=	ane	0	0	0	ane	0	one

As can exist seen in the example higher up, the process of binary multiplication is the same equally information technology is in decimal multiplication. Notation that the 0 placeholder is written in the 2nd line. Typically the 0 placeholder is non visually present in decimal multiplication. While the same can be done in this example (with the 0 placeholder beingness assumed rather than explicit), it is included in this example because the 0 is relevant for whatever binary add-on / subtraction reckoner, like the ane provided on this page. Without the 0 being shown, it would exist possible to make the fault of excluding the 0 when calculation the binary values displayed above. Annotation once more that in the binary organization, any 0 to the right of a ane is relevant, while whatever 0 to the left of the last ane in the value is not.

EX:

i 0 1 0 ane one 0 0
= 0 0 1 0 1 0 one i 0 0
≠ 1 0 1 0 1 i 0 0 0 0

Binary Division

The process of binary division is similar to long division in the decimal system. The dividend is notwithstanding divided past the divisor in the aforementioned manner, with the only significant deviation being the use of binary rather than decimal subtraction. Note that a good understanding of binary subtraction is of import for conducting binary division. Refer to the example below, besides as to the binary subtraction section for description.

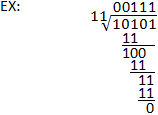
1 4 Of 20 Equals,

Source: https://www.calculator.net/binary-calculator.html

Posted by: rosadotorty1998.blogspot.com

Share this post